This post documents a compact pipeline to compute forward kinematics (FK) and inverse kinematics (IK) for the Dobot Magician Lite, and to execute accurate pick-and-place motions.
- Robot: Dobot Magician Lite (3-DOF arm + end-effector)
- Goal: Convert task-space waypoints into joint trajectories using IK, verify poses via FK, and run repeatable pick-and-place.
Demo: Pick and Place using Dobot Magician Lite
Below are short demonstrations of the pick-and-place routine running on the Dobot Magician Lite. They highlight the waypointing strategy and grasp/placing phases.
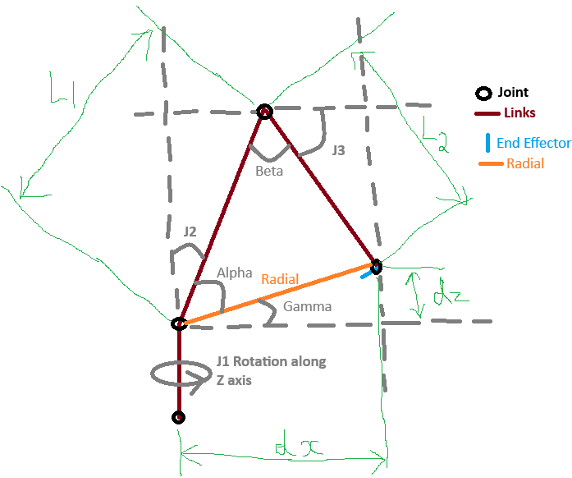
Kinematic Model
- Frames: Base (B), Shoulder (S), Elbow (E), Wrist (W), Tool (T)
- DH parameters: Denavit–Hartenberg convention to define link transforms.
Ti_{i-1}^{i} = Rot(z, θ_i) · Trans(z, d_i) · Trans(x, a_i) · Rot(x, α_i)
You can either obtain the official DH parameters from the vendor documentation or measure the effective link lengths and offsets. For small desktop arms, a good practice is to calibrate link lengths by probing a few known poses.
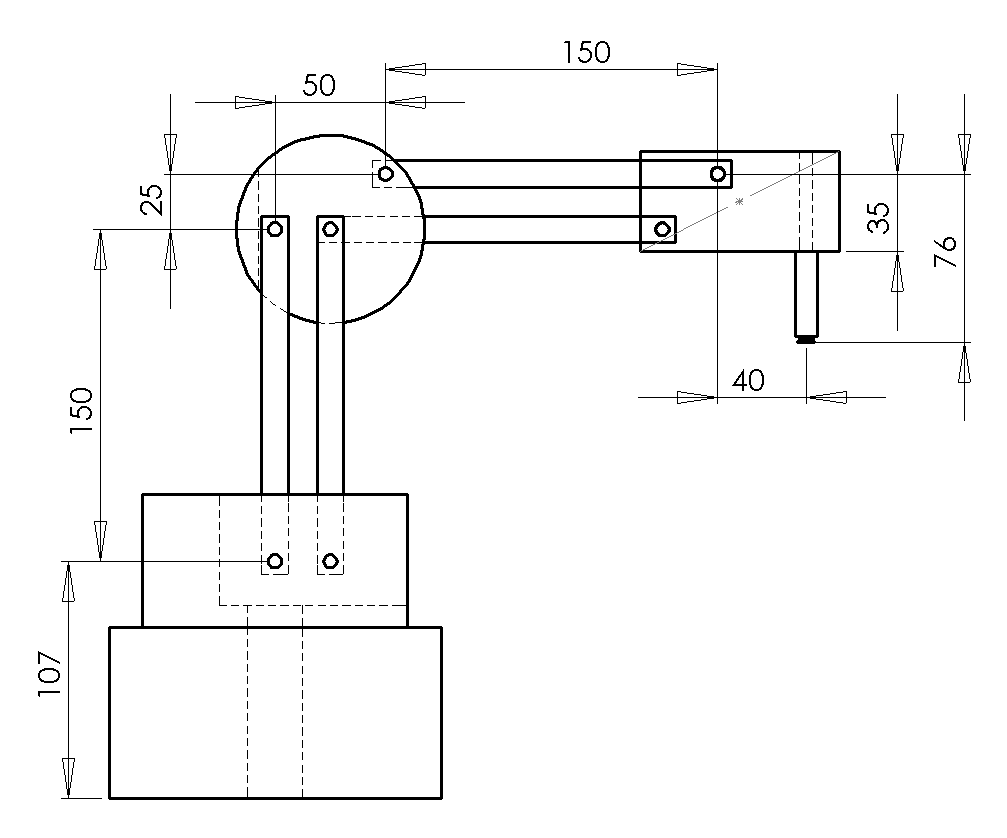
Dobot Magician Lites link length are 150mm each and has a X axis offset of 50 and no Z axis offset since the Z axis is measurement of the servo motor and not the TCP.
Important to note the limitation of joints

Forward Kinematics (FK)
def fk_deg(j1d,j2d,j3d,j4d):
"""
fk
x can be given by cosine of radius
y can be given by sine of radius
z can be given by z0+
"""
j1,j2,j3,j4 = map(rad,(j1d,j2d,j3d,j4d))
print(j1,j2,j3,j4)
rr = X0 + L1*math.sin(j2) + L2*math.cos(j3)
z = Z0 + L1*math.cos(j2) - L2*math.sin(j3)
x,y = rr*math.cos(j1), rr*math.sin(j1)
r = j1 + j4
return x,y,z,deg(r)
The above will give roughly 1-2mm of error but works under 1mm for most cases.
However a point can be made here by using geometric method and relying on it can be hard when number fo joints explode in a system and there you may want to consider usign,
FK composes the homogeneous transforms to obtain the tool pose from joint angles q = [q1, q2, q3].
import numpy as np
def dh(a, alpha, d, theta):
ca, sa = np.cos(alpha), np.sin(alpha)
ct, st = np.cos(theta), np.sin(theta)
return np.array([
[ct, -st*ca, st*sa, a*ct],
[st, ct*ca, -ct*sa, a*st],
[ 0, sa, ca, d],
[ 0, 0, 0, 1],
])
# Example placeholders (replace with your DH table)
# a = [a1, a2, a3]; alpha = [α1, α2, α3]; d = [d1, d2, d3]
# def fk(q):
# T01 = dh(a1, α1, d1, q[0])
# T12 = dh(a2, α2, d2, q[1])
# T23 = dh(a3, α3, d3, q[2])
# T0T = T01 @ T12 @ T23
# return T0T
Inverse Kinematics (IK)
For a planar 2R subsection (shoulder–elbow) plus a wrist alignment, you can derive a closed-form IK to reach (x, y, z) with a target tool pitch. The simplified 3-DOF IK (ignoring wrist roll) is often sufficient for pick-and-place.
Steps:
- Project target into the arm plane; compute shoulder angle with
atan2. - Law of cosines for elbow angle from link lengths and projected reach.
- Wrist angle to satisfy desired pitch or to keep the tool vertical.
def ik_deg(x,y,z,rd, elbow="down"):
j1 = math.atan2(y,x)
j4 = rad(rd) - j1
dr = math.hypot(x,y) - X0
print(f"dr {dr}")
dz = z - Z0
print(f"dz {dz}")
r2 = dr*dr + dz*dz
print(f"r2 {r2}")
r1 = math.sqrt(max(0.0,r2))
print(f"r1 {r1}")
# elbow selection via sign of sin(beta)
cB = (r2 - L1*L1 - L2*L2)/(-2*L1*L2); cB = max(-1.0,min(1.0,cB))
print(f"cB {cB}")
sB = math.sqrt(max(0.0,1-cB*cB))
print(f"sB {sB}")
if elbow=="up": sB = -sB
beta = math.atan2(sB, cB)
print(f"beta {beta}")
alpha = math.asin(L2*sB / (r1 if r1>1e-9 else 1.0))
print(f"alpha {alpha}")
gamma = math.atan2(dz, dr if abs(dr)>1e-9 else 1e-9)
print(f"gamma {gamma}")
j2 = math.pi/2 - alpha - gamma
print(f"j2 {j2}")
j3 = math.pi - beta - alpha - gamma
print(f"j3 {j3}")
return [deg(j1),deg(j2),deg(j3),deg(j4)]
Waypoints and Pick-and-Place Sequence
- Approach above pick:
(x, y, z + z_clear) - Descend to pick:
(x, y, z)and close gripper - Lift: back to
(x, y, z + z_clear) - Approach above place:
(x', y', z' + z_clear) - Descend to place:
(x', y', z')and open gripper - Retreat
Between waypoints, generate a time-parameterized joint trajectory with velocity/acceleration limits. Verify each pose via FK before commanding the hardware.
Implementation Notes
- Use Dobot SDK for command streaming and IO control (gripper/suction).
- Calibrate home pose and define a safe workspace box to avoid singularities/self-collisions.
- Add soft limits on
qanddq. - For higher accuracy, refine link lengths via least-squares from measured poses.
Next Steps
- Add camera-based detection for dynamic pick points.
- Blend linear segments (S-curve) to reduce jerk.
- Publish a small Python package with FK/IK utilities for Dobot Magician Lite.